Plot the trajectory of Apophis

Plot the close approach of Apophis in 2029.

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

import kete

# load apophis from horizons
obj = kete.HorizonsProperties.fetch("Apophis")
cur_state = obj.state
non_grav = obj.non_grav


jd_center = kete.Time.from_ymd(2029, 4, 13.9066).jd
jd_start = jd_center - 1.25
jd_end = jd_center + 1.25
steps = 1 / 24 / 60

# propagate the state up to the start date.
cur_state = kete.propagate_n_body(
    cur_state, jd_start, non_gravs=[non_grav], include_asteroids=True
)

# Now we propagate the object, recording info as we go
# this is not the most efficient way to do this, but for 1 object it is easy.
pos = []
dist_to_earth = []
moon_pos = []
dist_to_moon = []
elements = []
time = []
while cur_state.jd < jd_end:
    # propagate the object, and include the massive main belt asteroids
    cur_state = kete.propagate_n_body(
        cur_state, cur_state.jd + steps, include_asteroids=True
    )
    time.append(cur_state.jd - jd_center)
    elements.append(cur_state.elements)
    rel_earth_state = cur_state.change_center(399)
    pos.append([rel_earth_state.pos.x, rel_earth_state.pos.y])
    # gets earths position and record the distances.
    moon = kete.spice.get_state("Moon", cur_state.jd, center=399).pos
    dist_to_moon.append((moon - rel_earth_state.pos).r * kete.constants.AU_KM)
    dist_to_earth.append(rel_earth_state.pos.r * kete.constants.AU_KM)
    moon_pos.append([moon.x, moon.y])

cmap = matplotlib.colormaps["magma"]
colors = [cmap(x / len(elements) * 0.8) for x in range(len(elements))]

print("Closest approach is on:")
print(kete.Time(jd_start + np.argmin(dist_to_earth) * steps).iso)

# Note that this is at 10 steps a day, so this is not an exact calculation
print(f"At a distance of about {np.min(dist_to_earth):0.0f} km")

Closest approach is on:
2029-04-13T21:44:30.239+00:00
At a distance of about 38012 km

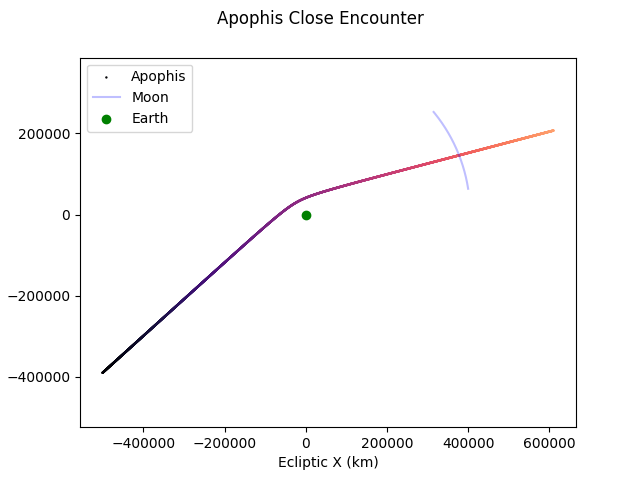
Top down view of solar system:

plt.suptitle("Apophis Close Encounter")
plt.scatter(*np.transpose(pos) * kete.constants.AU_KM, s=0.5, label="Apophis", c=colors)
plt.plot(
    *np.transpose(moon_pos) * kete.constants.AU_KM, c="blue", alpha=0.25, label="Moon"
)
plt.gca().axis("equal")
plt.scatter(0, 0, c="Green", label="Earth")
plt.xlabel("Ecliptic X (km)")
plt.ylabel("Ecliptic Y (km)")
plt.legend(loc=2)
plt.show()

Orbital elements change:

plt.figure(figsize=(6, 6))
plt.subplot(321)
plt.scatter(time, dist_to_earth, c=colors, s=2)
plt.yscale("log")
plt.ylabel("Distance to Earth (km)")

plt.subplot(322)
plt.scatter(time, dist_to_moon, c=colors, s=2)
plt.yscale("log")
plt.ylabel("Distance to Moon (km)")

plt.subplot(323)
ecc = [e.eccentricity for e in elements]
plt.scatter(time, ecc, c=colors, s=2)
plt.ylabel("Eccentricity")

plt.subplot(324)
inc = [e.inclination for e in elements]
plt.scatter(time, inc, c=colors, s=2)
plt.ylabel("Inclination (Deg)")
plt.xlabel("Time (Days)")

plt.subplot(325)
a = [e.semi_major for e in elements]
plt.scatter(time, a, c=colors, s=2)
plt.ylabel("Semi-Major Axis")
plt.xlabel("Time (Days)")

plt.subplot(326)
a = [e.peri_dist for e in elements]
plt.scatter(time, a, c=colors, s=2)
plt.ylabel("Perihelion Distance (AU)")
plt.xlabel("Time (Days)")

plt.tight_layout()
plt.show()